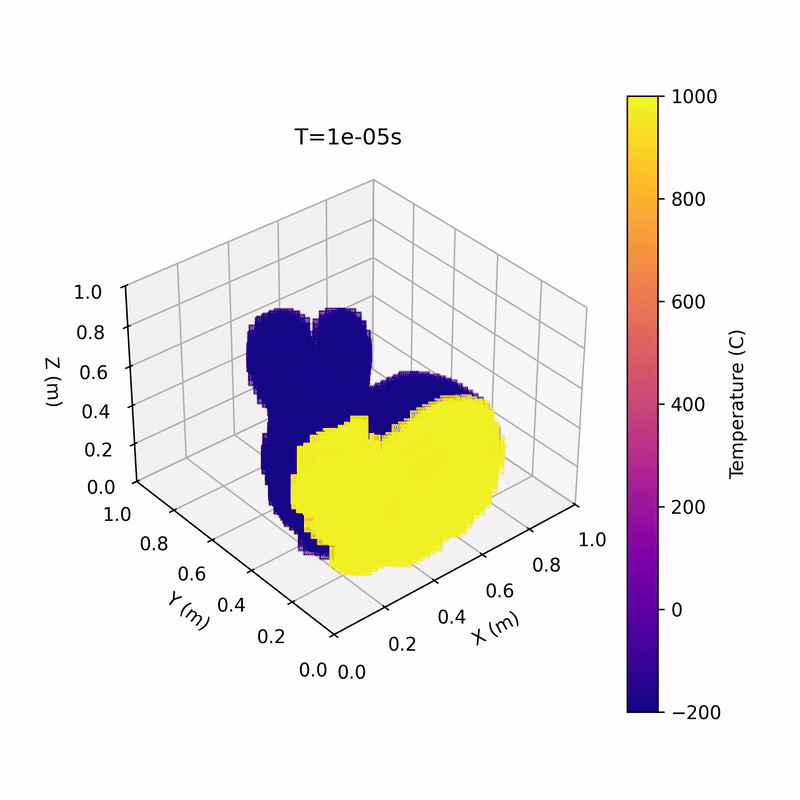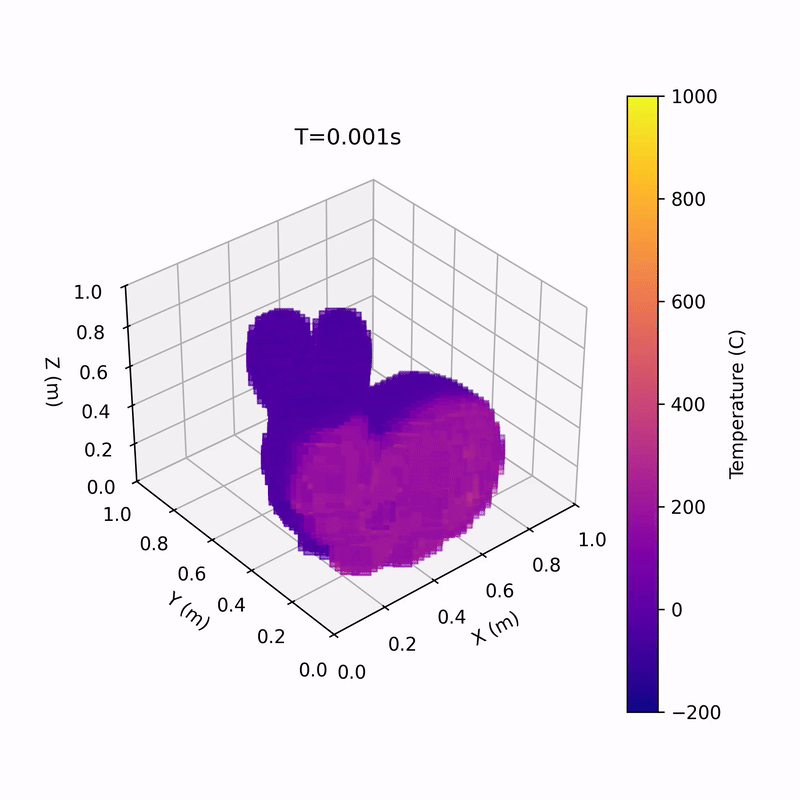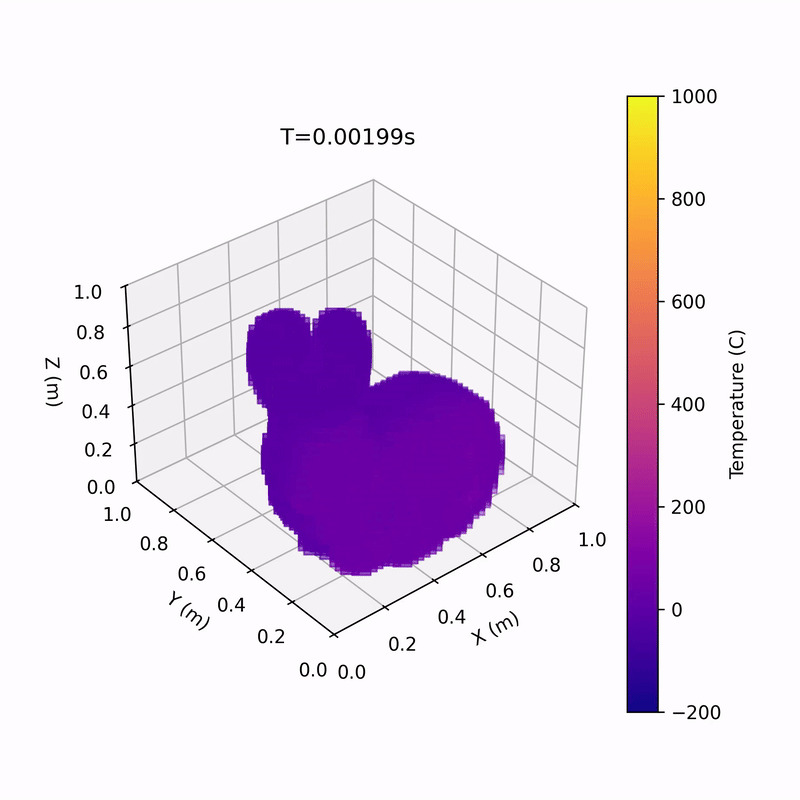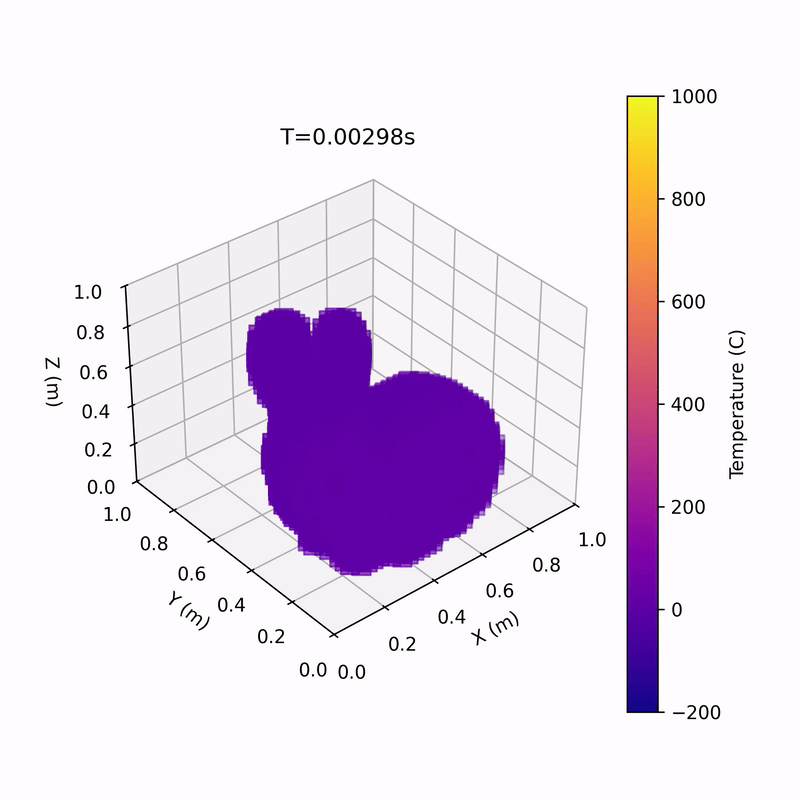
Multiprocessing 3D Heat Equation Solver
Github Repo
Quick Overview:
This program simulates heat transfer by numerically solving the heat equation via the Finite Difference Method. Space and time are discretized into finite intervals in order to approximate solutions to the system.
$$
\frac{\partial{u}}{\partial{t}} = \alpha\nabla^{2}u \\
\frac{\partial{u}}{\partial{t}} = \alpha\left(\frac{\partial^{2}{u}}{\partial{x^2}} + \frac{\partial^{2}{u}}{\partial{y^2}} + \frac{\partial^{2}{u}}{\partial{y^2}} \right)
$$
We can use this approximation:
$$
\frac{d^{2}f}{dx^2} \approx \frac{f(x+h) - 2f(x) + f(x-h)}{h^2}
$$
And solve for the next state of a cell:
$$
\frac{u^{i,j,k}_{t+\Delta t} - u^{i,j,k}_{t}}{\Delta t} = \alpha\left(\frac{u^{i+\Delta h,j,k}_{t} - 2u^{i,j,k}_{t} + u^{i-\Delta h,j,k}_{t}}{(\Delta h)^2} + ...\right) \\
u^{i,j,k}_{t+\Delta t} = \alpha\Delta t \left(\frac{u^{i+\Delta h,j,k}_{t} - 2u^{i,j,k}_{t} + u^{i-\Delta h,j,k}_{t}}{(\Delta h)^2} + ...\right) + u^{i,j,k}_{t}
$$
Multiprocessing!
For a 3D grid of cells, many of these calculations will be needed. What this program does is create an array in shared memory that represnets some 3D grid space and splits off into many child processes, each of which work on a separate "layer" of the grid. This was very fun to work out and get together.
How to use!
To compile:
$ make
To run:
$ ./solver input.csv output.csv
A note
This is not really a bug, but make sure that your dt/(units^2) is less than 0.5. If this value is above 0.5, the system will not be numerically stable. read more about it here
Using the description language:
python venv (python3 3.10 used)
set up the virtual environment
$ python3 -m venv .env
Install dependencies:
$ pip3 install -r visualizer/requirements.txt
Activate the environment
$ source .env/bin/activate
Syntax
Statements are seperated by semicolons
SIZE x y z (m);
//define the size of the space (must be first line of program)
MAT name thermal-coeff (m^2/s);
//define a material
TI t (s);
//define time_initial
TF t (s);
//define time_final
DT t (s);
//define time step
UNITS t (m);
//define meters-per-cell
//The above paramters must be defined before anything else!
SETTEMP temp (C) x0 y0 z0 x1 y1 z1 (m);
//sets a box defined by opposing corners (x0, y0, z0) and (x1, y1, z1) to a certain temperature
BOX material temp (C) x0 y0 z0 x1 y1 z1 (m);
//creates a box of some material and some initial temperature
SPHERE material temp (C) cx cy cz radius (m);
//Creates a sphere of some material and some initial temperature with center (cx, cy, cz) and radius (m)
MESH file.stl x-len material temp (C) x y z (m);
//voxelizes a .stl file and places the lower-left-corner of it's bounding box at x y z. The file is the path from the cwd, the x-len is a scaling factor (sets how long the bounding box is along the x-axis).
Note that DT/(UNITS^2) < 0.5 MUST BE TRUE! try to minimize this value.
Example program
UNITS 0.025;
TI 0.0;
TF 0.01;
DT 0.00001;
SIZE 1 1 1;
MAT m1 0.5;
SETTEMP 32 0 0 0 1 1 1;
BOX m1 32 0 0 0 1 1 0.1;
SETTEMP 1000 0.2 0.2 0 0.8 0.8 0.1;
Converting description language to .csv input file
$ ./setup input.sim output.csv
This will display a preview of the environment in a numpy window (lets you get the proper elevation and azimuth angles)
Visualizing data
$ ./render data.csv dirname
Numbered images will be written to the dirname.
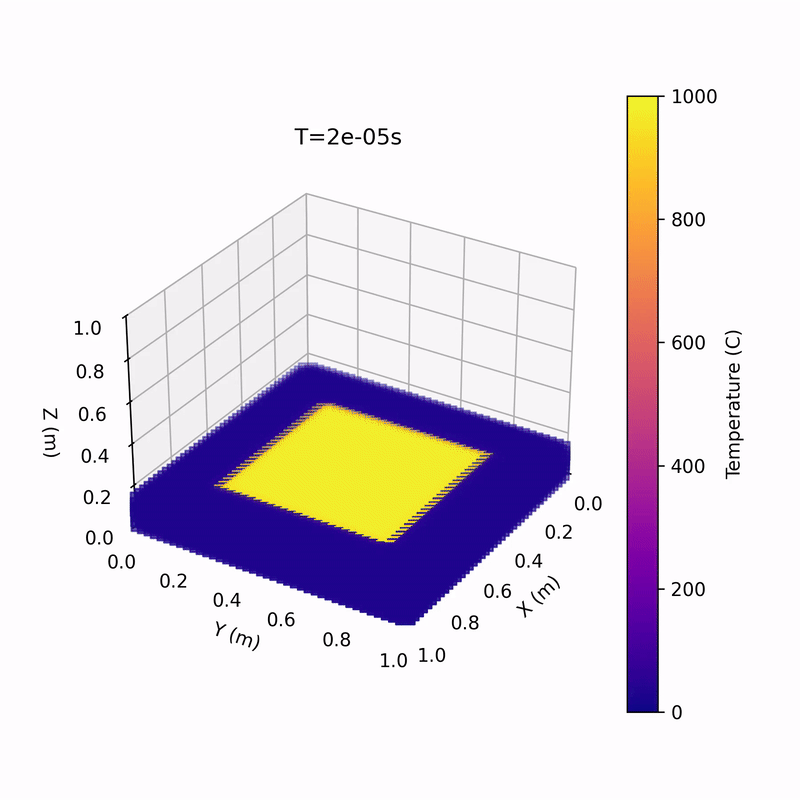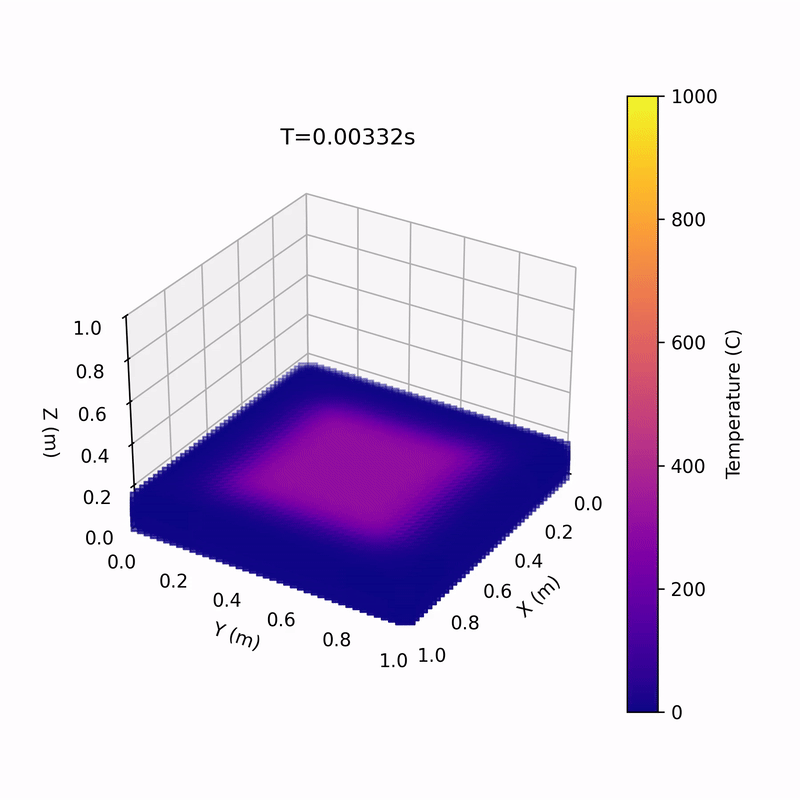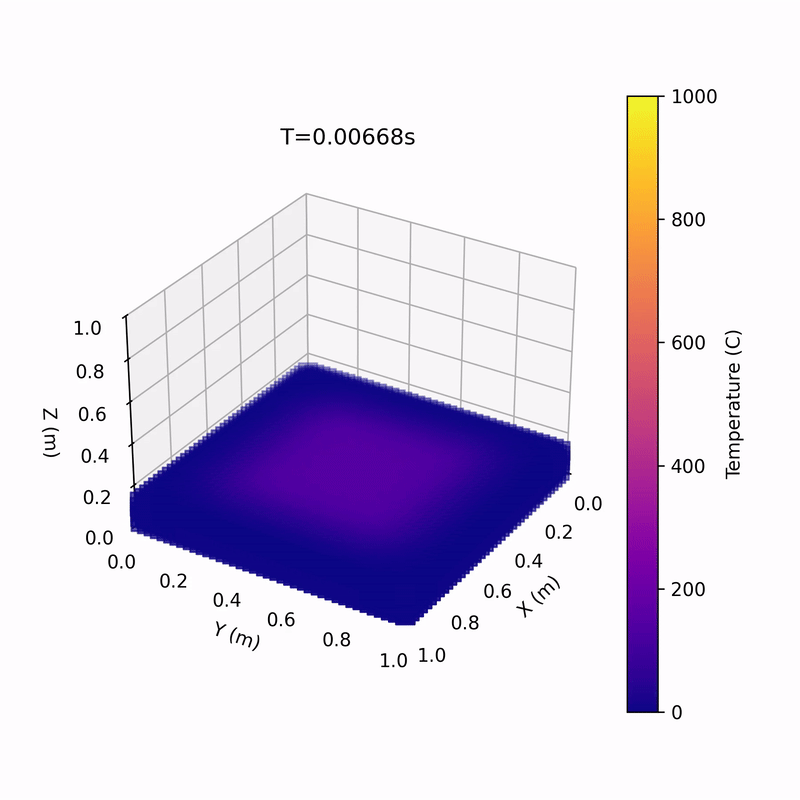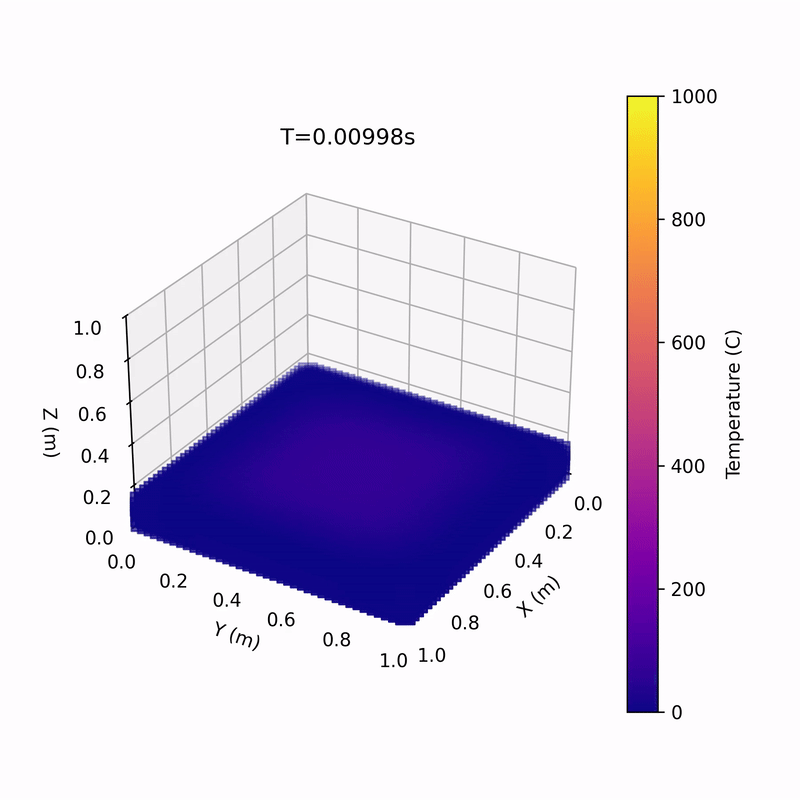
Media!